Tổng hợp các hình trong toán học lớp 1, tổng hợp các loại hình học cơ bản

Hình học không khí là một dạng toán quan trọng, tuy vậy đây là một phạm trù khá thử thách đối với rất nhiều các bạn học sinh. Để nắm vững kiến thức này, những em học viên hãy cùng VUIHOC ôn lại vững phần lý thuyết và cách giải các dạng bài tập từ cơ bản đến cải thiện nhé!

1. Hình học không khí là gì?

Hình học không khí được biết là thuộc nhánh thuộc hình học nghiên cứu các đối tượng trong không khí ba chiều Euclid.

Bạn đang xem: Các hình trong toán học

Bên cạnh đó, hình học khối tích (Stereometry) nghiên cứu các phép tính về thể tích của nhiều khối đặc khác nhau (các khối trong không khí 3 chiều) như: thể tích khốilăng trụ, khối chóp, hình cụt, các khối giới hạn bởi mặt cầu, các nhiều diện, hình trụ tròn, hình nón.

Các nhà đề bao gồm trong hình học không gian gồm có: góc khối, hình lập phương, hình hộp chữ nhật, tứ diện và các loại hình chóp, hình lăng trụ, mặt cầu, quan tiền hệ giữa mặt phẳng và đường thẳng,...

2. Những dạng hình học không khí thường gặp

Hình học không gian được tế bào phỏng trong không gian ba chiều, tạo thành khối trụ (được cấu tạo từ nhiều mặt phẳng) cố kỉnh vì một mặt phẳng.

Các bài toán về hình học không gian thường gặp là: tính diện tính toàn phần, diện tích bao phủ hay thể tích.

Dạng 1: Hình hộp chữ nhật

Có sáu mặt đều là hình chữ nhật

Dạng 2: Hình lập phương

Hình lập phương có 6 mặt đều là hình vuông.

Dạng 3: Hình lăng trụ

Hình có hai đáy là hình tam giác, các mặt còn lại là hình bình hành.

Dạng 4: Hình khối chóp

Hình khối chóp được sinh sản ra bằng phương pháp kết nối một điểm của một nhiều giác và một điểm. Các tam giác được tạo ra được gọi là cạnh bên.

Dạng 5: Hình cầu

Là phần phía trong một mặt phẳng gồm các điểm trong không gian nằm phương pháp tâm một khoảng cách không đổi.

Dạng 6: Hình trụ

Được vẽ thành do hai lòng là hai hình trụ bằng nhau. Lúc quay hình chữ nhật quanh một cạnh thắt chặt và cố định thì chúng ta sẽ được một hình trụ.

Dạng 7: Hình nón

Là hình được hình thành vì một tam giác vuông quay quanh trục của nó.

3. Giải pháp học tốt và giải bài xích tập hình học không khí nhanh nhất

3.1. Nỗ lực vững lý thuyết hình học tập không gian

3.2. Làm nhiều bài tập

Khi luyện đề, các em học viên cần lưu giữ ý những điều sau:

Đọc kĩ đề bài

Nên chú ý các ý vào đề bài vì bỏ sót ý sẽ dần đến ko hoàn thành câu hỏi.

Khi bài xích cho tài liệu “Cho hình chóp đều cạnh a”. Vào đầu chúng ta cần buộc phải nghĩ ngay đến những kiến thức liên quan như: “chân đường cao trùng cùng với đáy”; “các cạnh bằng nhau”, “ các mặt bên bằng nhau”,…

Nếu trong bài bác có mang đến “mặt bên là tam giác cân”, từ bây giờ học sinh nên sử dụng kiến thức và kỹ năng về hình học phẳng để vận dụng. Một tam giác cân nặng thì sẽ có được đường cao đồng thời là trung tuyến,…

Cách tốt nhất khi hiểu đề, học sinh hãy liệt kê ra toàn bộ thông tin đề đã cho và yêu ước của đề. Tự yêu ước của bài những em đã suy trái lại những kiến thức cần sử dụng.

Luyện sự sáng tạo khi học tập hình không gian

Luyện sự trí tuệ sáng tạo chính là phương pháp để học xuất sắc hình học tập không gian. Trong tương đối nhiều bài những em sẽ rất cần phải kẻ thêm hình mà trong bài không còn cho trước.

Khi kẻ thêm mặt đường thẳng, thêm phương diện phẳng thì vấn đề giải bài xích sẽ trở nên tiện lợi hơn. Mặc dù điều này buộc phải sự sáng tạo từ các em.

Để dành được sự sáng tạo này những em bắt buộc làm nhiều dạng bài, tìm hiểu thêm các cách giải không giống nhau. Trường đoản cú đó các em rất có thể hình thành nên thói thân quen tập bốn duy vẽ thêm hình khi làm bài bác tập. Phối hợp các dạng bài với nhau để có được nhiều phương pháp giải bài xích nhanh cùng hay hơn.

Luyện cách nhìn hình

Học sinh đề xuất luyện tập ý kiến hình nhằm giải nhanh bài bác tập.

Luyện ý kiến hình là giữa những bước cơ bản đầu tiên để hoàn toàn có thể giỏi hình học không gian.

Chỉ khi bạn cũng có thể nhìn rõ những mặt phẳng, đường thẳng thì mới rất có thể áp dụng định lý, hệ quả nhằm suy ra biện pháp giải.

Ở bước này các em cần để ý đến sự ảnh hưởng của mình. Hãy liên can đến nơi ở với các góc, bức tường,… hệt như các góc, các đường thẳng với mặt phẳng trong ko gian.

Trong hình học đặc biệt quan trọng là sự hình dung, tưởng tượng. Nếu vẫn thành thục bước này thì các em đã rất văn minh và ở đoạn học vẽ hình tiếp sau sẽ không thể khó.

3.3. Biết phương pháp vẽ hình học tập không gian

Hiểu rằng vẽ sai hình sẽ ko được tính điểm lúc làm bài hình học không gian.

Hiểu quy tắc: vẽ nét đứt khi bị khuất, vẽ nét liền khi nhìn thấy. đề nghị vẽ hình bằng bút chì, bởi vì nét đứt, nét liền có thể núm đổi vào quá trình làm bài.

Các bước cần làm theo khi vẽ hình:

Nên đọc kĩ đề trước lúc vẽ hình để không bị nhầm, lựa chọn cách vẽ làm thế nào để cho phù hợp

Nên vẽ mặt phẳng đầu tiên theo dạng hình bình hành. Những đường thẳng vào mặt phẳng cắt ngang nên chếch về trái hoặc phải. Yêu cầu cắt về phía trước, hạn chế cắt về phía sau.

Những phần bị lấp vào hình: đường thẳng, mặt phẳng vẽ bằng nét đứt, cần sử dụng nét liền lúc phần hình không xẩy ra che.

Khi vẽ hình chóp: mặt đáy: vẽ dẹt, mỏngt, mặt dưới được vẽ quá to sẽ khiến cho nhìn không thật, khó nhìn.

Nên vẽ với nhiều góc nhìn khác nhau, biến đổi đỉnh, khía cạnh phẳng đáy, mặt phẳng bên,… Nếu chỉ vẽ 1 hình mà khó nhìn thì sẽ ko nhìn ra.

Các cụ thể nên được diễn đạt rõ ở khía cạnh đáy, giảm bớt vẽ vào mặt chết thật sẽ khiến các em khó tưởng tượng được bài.

3.4. Biết các cách giải bài bác tập toán hình học không khí nhanh

Bài toán 1: Tìm giao tuyến giữa nhị mặt phẳng
Điểm thông thường thứ nhất thường dễ nhận biết.
Điểm phổ biến thứ hai: Giao của nhị đường còn lại.
Ví dụ 1:
Cho tứ giác ABCD làm sao cho các cạnh đối không tuy nhiên song với nhau. Rước một điểm S ko thuộc mặt phẳng (ABCD). Khẳng định giao tuyến của nhì mặt phẳng:
a) mặt phẳng (SAC) và mặt phẳng (SBD).
b) mặt phẳng (SAB) với mặt phẳng (SCD).
c) khía cạnh phẳng (SAD) cùng mặt phẳng (SBC)
Giải:
Bài toán 2: Tìm giao điểm của mặt phẳng và đường thẳng
Tìm giao điểm của của dường thẳng a với một đường thẳng khácb, vào mặt phẳng (P).
Xem thêm: Cách Dùng Hàm Left Và Right, Hàm Left/Right: Công Thức, Cách Dùng Trong Excel
Nếu không tìm được đường thẳng đó.
Tìm một mặt phẳng khác (Q) chứa đường thẳng đề bài đến (P).
Tìm giao tuyến b của mặt phẳng đó với mặt phẳng đã mang lại (P).
A là giao của a và b thì A sẽ là giao của a và (P).
Ví dụ:
Cho tứ diện ABCD. Call E với F theo lần lượt là trung điểm của AB với CD; G là giữa trung tâm tam giác BCD. Tra cứu giao điểm của mặt đường thẳng EG cùng mặt phẳng (ACD).
Giải:
Ta tất cả G là giữa trung tâm tam giác BCD; F là trung điểm của CD buộc phải G ∈ BF ⊂ (ABF)
+ E là trung điểm của A B E ∈ (ABF).
+ chọn mp phụ chứa EG là (ABF).
Giao tuyến của (ACD) cùng (ABF) là AF
Trong mp(ABF); điện thoại tư vấn M là giao điểm của EG cùng AF.
Giao điểm của EG với mp(ACD) là giao điểm M của EG với AF
Bài toán 3: Chứng mình bố điểm thẳng hàng
Ta cần chứng mình các điểm ấy thuộc nhị mặt phẳng riêng biệt.
Ví dụ:
Cho tứ diện SABC. Gọi L; M; N theo lần lượt là các điểm trên những cạnh SA; SB cùng AC sao cho LM không song song cùng với AB với LN không tuy nhiên song với SC. Phương diện phẳng (LMN) cắt những cạnh AB; BC và SC theo lần lượt tại K; I; J. Minh chứng 3 điểm M, I, J thẳng hàng?
Giải
Ta có
M ∈ SB ⇒ M isin; (LMN) ∩ (SBC)(1)
I ∈ BC ⊂ (SBC) cùng I ∈ NK ⊂ (LMN)
⇒ I ∈ (LMN) ∩ (SBC)(2)
J ∈ SC ⊂ (SBC) và J ∈ LN ⊂ (LMN)
⇒ J ∈ (LMN) ∩ (SBC)(3)
⇒ M ; I; J thẳng hàng vì cùng ở trong giao con đường mp (LMN) với (SBC)
Bài toán 4: Dựng thiết diện của một mặt phẳng (P) và khối đa diện (T)Đi tìm giao tuyến của (P) và (T).
Kéo dài giao tuyến đã có, tìm giao điểm với các cạnh của mặt này, tương tự, tìm được các giao tuyến còn lại. Nối thành đường khép kín sẽ có thiết diện ta cần tìm.
Ví dụ:
Cho tứ diện ABCD; hotline H với K theo thứ tự là trung điểm của AB cùng BC. Trê tuyến phố thẳng CD đem điểm M nằm quanh đó đoạn CD. Tiết diện của tứ diện cắt vị mặt phẳng (HKM) là?
Giải:
Mặt phẳng (BCD) gồm KM không song song với CD nên gọi L là giao điểm của KM và BD.
Ta có: (HKM) ∩ (ABC) = HK
(HKM) ∩ (BCD) = KL
(HKM) ∩ (ABD) = HL
Vậy thiết diện là tam giác HKL.
Bài toán 5: Chứng minh một đường thẳng trải qua một điểm cố định có sẵn
Chứng mình đường thẳng đó: a là giao của nhị mặt phẳng (P) và (Q).
Một mặt phẳng đi qua một đường thẳng b cố định.
Khi đó a đi qua I cố định là giao của (P) và b.
Ví dụ:
Giải
Bài toán 6: Chứng mình đường thẳng:a tuy vậy song mặt phẳng: (Q)
Tìm mp (Q) chứa a
Tìm b là giao của (P) và (Q)
Khi đó chứng mình a//b
Ví dụ:
Cho tứ diện ABCD. Gọi G là trung tâm của tam giác ABD; Q nằm trong cạnh AB làm thế nào để cho AQ = 2QB; gọi p là trung điểm của AB. Chứng tỏ GQ // mp(BCD).
Giải:
Gọi M là trung điểm của BD
Vì G là trung tâm tam giác ABD nên AG/AM = 2/3 (1)
Điểm Q thuộc AB thỏa mãn: AQ = 2QB đề xuất AQ/AB = 2/3 (2)
Từ (1) và (2) suy ra: AG/AM = AQ/AB
⇒ GQ // BD (định lí Ta-let đảo)
Mặt khác BD phía bên trong mặt phẳng (BCD) suy ra GQ // mp(BCD)
Để hiểu hơn về hình học không gian cũng giống như thành thạo các bài tập giải hình không gian, thầy Tài sẽ có bài giảng "hack điểm" hình không gian cực hay. Chúng ta học sinh cùng xem và học cùng thầy trong video clip này nhé!
Như vậy, trong nội dung bài viết này VUIHOC đã chia sẻ về tư tưởng hình học không gian cũng tương tự các dạng toán hay gặp, hơn không còn là những cách giải toán dễ hiểu nhất. Hy vọng các em sẽ có thêm những bí quyết và nâng cấp kiến thức của chính mình trong kỳ thi THPTQG tới đây nhé. Để rèn luyện thêm những dạng toán, các em truy cập vào vuihoc.vn với đăng ký khóa đào tạo và huấn luyện ngay bây chừ nhé!
Bài viết sau đây để giúp đỡ trẻ hệ thống lại được kỹ năng và kiến thức về những hình trong toán học lớp 1 dễ dàng và nhanh chóng nhất.

Trong lịch trình toán học lớp 1, cạnh bên phần đại số thì trẻ cũng sẽ được tập có tác dụng quen với mọi dạng toán hình học. Vậy trẻ sẽ tiến hành học đông đảo hình học tập nào? Trong bài viết này chuyenly.edu.vn sẽ hỗ trợ đến quý phụ huynh cùng thầy cô những hình trong toán học lớp 1 giúp trẻ hoàn toàn có thể hệ thống lại kiến thức và kỹ năng một biện pháp nhanh chóng.
1. Toán hình học tập lớp 1 gồm gồm những kỹ năng nào?
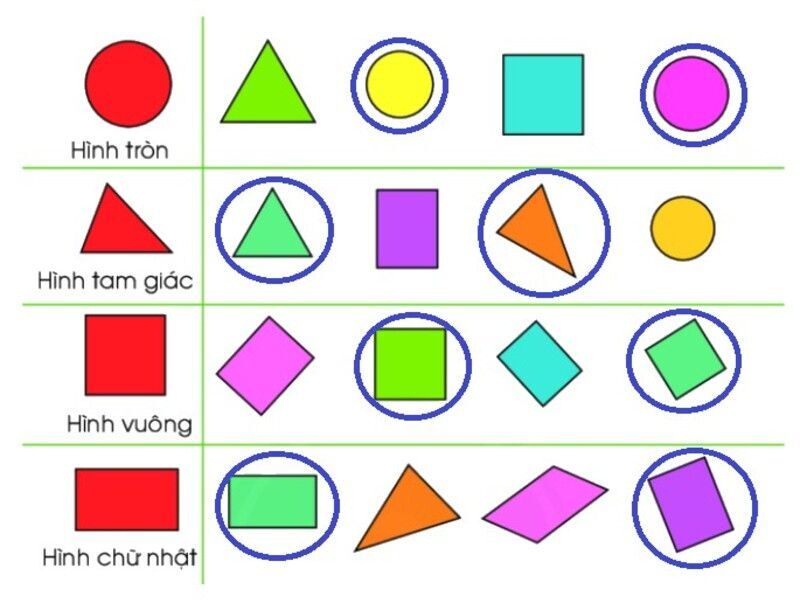
Các hình vào toán học tập lớp 1 sẽ bao hàm những kỹ năng và kiến thức cơ phiên bản như:
Điểm: điểm đó là một tư tưởng cơ bạn dạng trong hình học tập với đa số hình ảnh là những chấm tròn mở ra ở xung quanh phẳng. Nhì điểm phân biệt hoàn toàn có thể tạo thành được một quãng thẳng. Fan ta hay sử dụng các chữ mẫu in hoa như A, B, C, D để tại vị tên cho những điểm này
Đoạn thẳng: đoạn trực tiếp được ra đời từ hai điểm rõ ràng với nhau. Cùng đoạn thẳng chính là cơ sở để xuất hiện nên các hình vuông, hình chữ nhật và hình tam giác,...
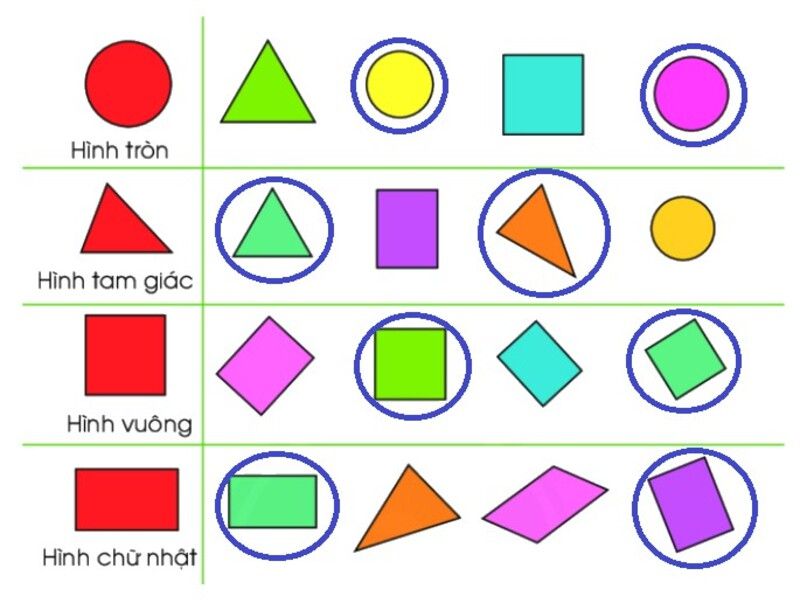
Hình vuông: Đây là một trong hình gồm bốn cạnh đều bằng nhau và có bốn góc vuông.
Hình tròn: là hình không có góc và không có cạnh nhưng đường bao quanh hình tròn đã là con đường cong kín.
Hình tam giác: là một hình có cha cạnh và có bố góc.
2. Các dạng bài bác tập về hình học toán lớp 1 giành riêng cho trẻ
Khi được học và làm cho quen về các hình trong toán học tập lớp 1 trẻ em sẽ chạm chán phải một số trong những dạng bài tập như:
2.1 nhận thấy hình học
Đây là 1 dạng toán cơ bạn dạng đầu tiên xuất hiện trong những bài tập liên quan tới kỹ năng lớp 1 về hình học mà trẻ sẽ gặp mặt phải. Để rất có thể làm được các dạng bài tập nhận ra hình học thì những bạn nhỏ tuổi chỉ cần ghi lưu giữ về quan niệm về điểm, đoạn thẳng và những hình cơ phiên bản như vậy sẽ có tác dụng được.
Trẻ chỉ việc nghe thầy gia sư giảng kỹ làm việc trên lớp là đã hoàn toàn có thể dễ dàng nhận biết được điểm, đoạn thẳng, hình vuông, hình tam giác hay hình tròn. Khi có tác dụng dạng bài tập này, trẻ sẽ tiến hành củng cụ thêm kiến thức và kỹ năng cho mình.
2.2 bài toán nhận thấy điểm
Dạng bài bác tập sản phẩm hai nhưng mà trẻ sẽ được học trong chương trình kiến thức toán lớp 1 về hình học chính là việc nhận biết được điểm ở trong giỏi ở ngoài so với một hình đến trước.
Nếu như những bạn nhỏ tuổi thấy một điểm hoặc thấy một quãng thẳng nằm trọn vẹn bên phía trong giới hạn của một hình thì đó đó là điểm hay là đoạn thẳng nằm phí trong hình. Còn ví như như điểm hoặc đoạn thẳng nằm tại vị trí ngoài giới hạn đó thì điểm cùng đoạn thẳng sẽ không nằm trong hình.
2.3 thực hành vẽ, giảm hoặc ghép các hình trong toán học lớp 1
Một dạng bài xích tập thực hành cũng rất thú vị mở hầu như các bạn nhỏ tuổi đều hết sức yêu thích khi tham gia học toán lớp 1 hình học tập đó chính là thực hành vẽ hoặc giảm ghép những hình. Đề bài xích sẽ yêu cầu các bạn phải vẽ hình, giảm một hình theo yêu ước hay có thể là ghép hình làm sao đó.
Nhiệm vụ của những em là chỉ cần làm theo là để ghi được điểm. Muốn làm được dạng bài bác tập này thì trước hết những bạn nhỏ dại nên tập vẽ hình thật nhiều. Vị kể cả so với các dạng bài bác tập giảm hình thì những con cũng nên biết vẽ hình rồi cắt theo con đường kẻ đang vẽ.
2.4 Đếm hình
Dạng toán thú vui tiếp theo cũng tương đối thường xuyên lộ diện trong những bài tập kiến thức và kỹ năng về hình học lớp 1 đó chính là đếm hình. Đối với dạng bài tập này thì những em rất cần được thật sự để ý trong khi làm.
Lý bởi vì là vì chưng đề bài bác thường sẽ khá ít khi đưa ra hồ hết hình riêng biệt để cho những bạn nhỏ đếm. Thay vào này sẽ đưa ra các hình chèn ghép với nhau để tăng sự bốn duy của trẻ. Cùng nhiệm vụ của các con đó là phải quan sát thật kỹ để đếm được hình chủ yếu xác.
3. Một trong những bài tập tổng hợp về những hình vào toán học tập lớp 1
Sau đây sẽ là một số trong những bài tập liên quan đến những hình trong toán học lớp 1 mà những bậc phụ huynh rất có thể tham khảo cho trẻ tự rèn luyện mỗi ngày:
Bài tập 1
Khoanh tròn vào hình vuông vắn ở giữa những hình sau đây:
Trong các hình sinh hoạt trên hình nào là hình vuông?
Bài tập 2
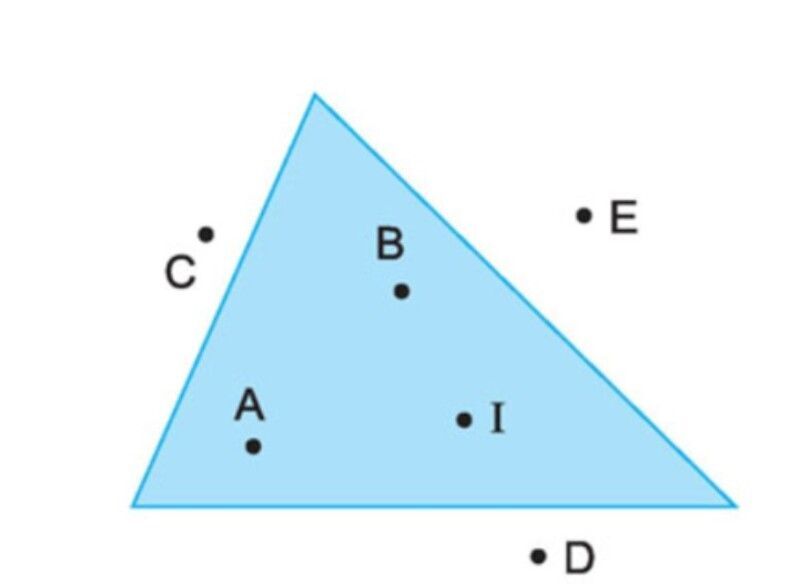
Điểm A ở phía trong hay bên phía ngoài của hình tam giác?
Bài tập 3
Vẽ một hình vuông vắn có cạnh nhiều năm là 4 cm.
Bài tập 4
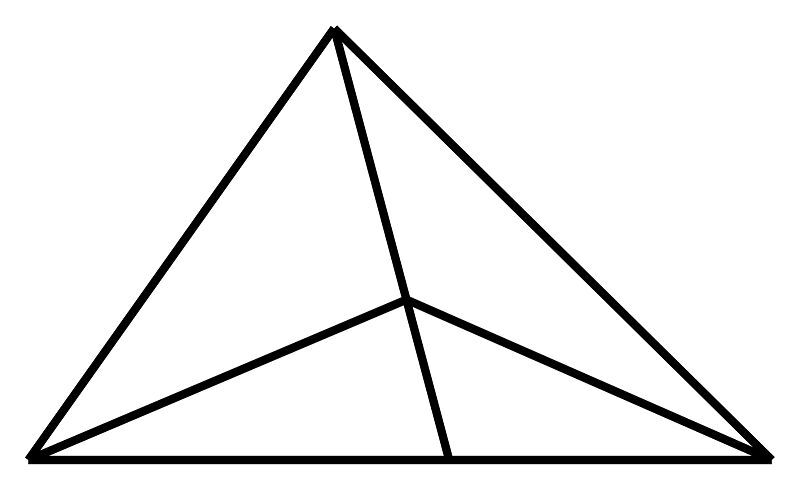
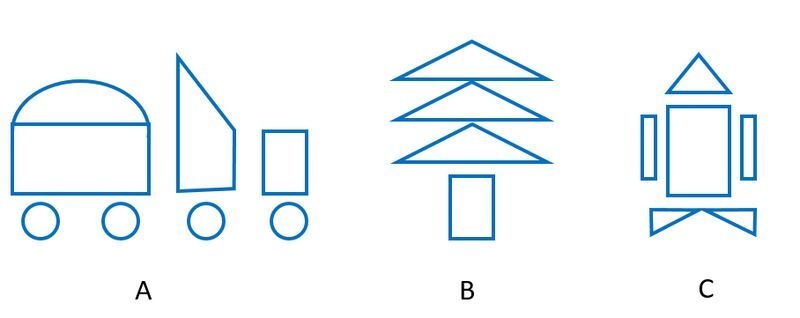
Có toàn bộ bao nhiêu hình tam giác ở mẫu vẽ trên?
Trên đấy là những thông tin về những hình vào toán học tập lớp 1 mà công ty chúng tôi muốn giữ hộ đến chúng ta đọc. Hi vọng với những share ở trên đã là tài liệu giúp cho quý phụ huynh cùng thầy cô hoàn toàn có thể giúp trẻ em học xuất sắc hơn mỗi ngày. Hãy thường xuyên xuyên truy cập vào website của chuyenly.edu.vn để có thêm các kiến thức hữu dụng nhé!