Sau những bài toán trên lớp hay các bài tập đã có thầy cô giáo huấn luyện và giảng dạy trên lớp, trên trường, liệu gồm bài toán cạnh tranh nhất vắt giới nào nhưng bạn không được biết? Hãy cùng khám phá xem đâu là những câu hỏi khó nhất trái đất để bạn cũng có thể biết thêm những thông tin có lợi và độc đáo hơn nha!
Lịch sử, xuất phát ra đời của toán học
Rất lâu trước khi lộ diện những văn tự cổ tốt nhất trên thế giới, đã có rất nhiều bức vẽ cho biết thêm có một kiến thức và kỹ năng về toán học tập và giải pháp đo thời gian dựa trên sao trời. Lấy ví dụ như các nhà cổ sinh vật học đã tò mò ra được các mảnh đất thổ hoàng trong một hang động nằm tại Nam Phi được tô điểm bởi những hình tương khắc hình học với thời gian khoảng 70.000 TCN.
Bạn đang xem: Giải các bài toán khó
Cũng những di khảo tiền sử đã được tìm thấy sinh hoạt châu Phi cùng nước Pháp, thời gian nằm khoảng chừng giữa 35000 TCN và 20000 TCN, cho biết thêm các cố gắng sơ khai của fan tiền sử nhằm định lượng thời gian.
Các minh chứng còn tồn tại cho đến ngày nay hầu như thấy việc đếm thời sơ khai nhà yếu là vì người phụ nữ, những người dân giữ những vật đánh dấu chu kỳ sinh học tập của bản thân hàng tháng; ví như hai mươi tám, nhì mươi chín, hoặc tía mươi vạch trên hòn đá hoặc xương hễ vật, theo kế tiếp là một vạch ngăn cách khác. Rộng nữa, các thợ săn thời cổ đại đã gồm khái niệm về một, nhị và những số nữa tương tự như không lúc chứng kiến tận mắt xét số lượng cá thể của bè cánh thú.
Xương Ishango được tìm thấy ở thượng nguồn dòng sông Nile (phía bắc lãnh thổ nước cộng hòa Dân nhà Congo), ở trong thời kì 20.000 TCN. Bản dịch phổ cập nhất của các hòn đá này cho biết nó là bởi chứng nhanh nhất có thể thể hiện tại một dãy các số nguyên tố với phép nhân của ai Cập cổ đại.
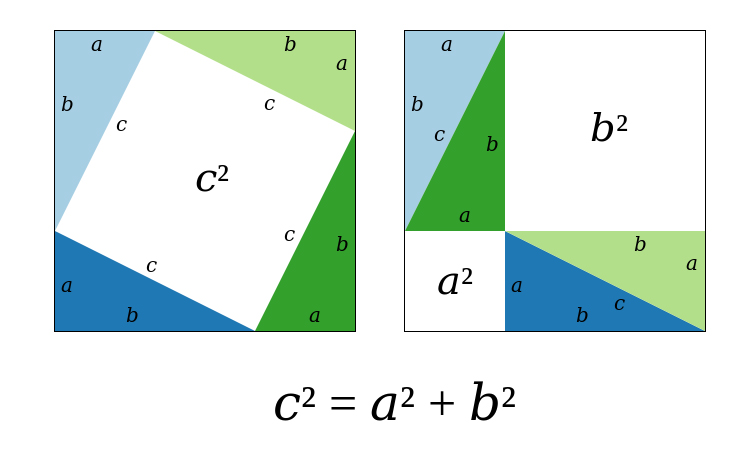
Vào thiên niên kỷ đồ vật 5 TCN, người Ai Cập cổ kính đã vẽ các bức tranh về thiết kế hình học và không gian. Bạn ta đã gửi ra những giả thuyết để xác định các hòn đá tế thần sống Scotland cùng Anh từ thiên niên kỷ lắp thêm 3 TCN, bao gồm cả các ý tưởng hình học tập như hình tròn, hình elip và bộ ba Pythagore trong thiết kế của nó.
Nền toán học sớm nhất được nhỏ người khám phá là sống Ấn Độ cổ đại nằm vào khoảng thời gian 3000 TCN – 2600 TCN ngơi nghỉ nền hiện đại thung lũng Indus (nền thanh lịch Harappa) của Pakistan với Bắc Ấn Độ. Nền toán học ở chỗ này đã cải tiến và phát triển một hệ thống các đơn vị đo.
Tại Thung lũng Indus cổ xưa đã đưa vào sử dụng hệ cơ số 10, một technology gạch đáng kinh ngạc khi sử dụng những tỉ lệ, các đường đi được bỏ lên trên một góc vuông cực kỳ hoàn hảo. Đồng thời một số trong những các hình hình học và thiết kế, bao hàm hình vỏ hộp chữ nhật, thùng phi, hình trụ, hình nón và các bức vẽ minh họa các hình tròn và hình tam giác cắt nhau với đồng quy.
Các dụng cụ dùng vào toán học do những nhà khảo cổ học tập tìm được bao gồm một thước đo cơ số 10 với độ chia nhỏ và cực kỳ chính xác. Đi kèm cùng với đó là một trong những dụng vắt vỏ sò được chuyển động như một mẫu com pa nhằm đo góc trên mặt phẳng hoặc theo những bội của góc 40 – 360 độ và một khí cụ vỏ sò khác nhằm đo 8-12 phần của mặt đường chân trời và thai trời. Tiếp đó là 1 trong bộ luật pháp để đo vị trí của các sao, các hình tinh nhằm mục đích định hướng. Phiên bản viết tay của fan Indus vẫn chưa được giải nghĩa; vì chưng đó họ biết được hết sức ít về những dạng viết của toán học Harappan.
Các minh chứng khảo cổ đã làm nhiều nhà sử học tập trên trái đất tin rằng nền thanh tao này đã thực hiện được hệ đếm cơ số 8 và đạt được các thành trái về kỹ năng và kiến thức tính tỉ lệ thân chu vi của mặt đường tròn so với bán kính của nó, do đó mà tính được số π chính xác nhất.
6 việc khó tuyệt nhất trên thế giới được con fan biết đến
Cộng đồng mạng từng đưa ra các tranh luận sôi nổi về những bài bác toán khi chứng kiến tận mắt qua tưởng chừng như rất dễ dàng của học tập sinh, nhưng lại trên thực tế lại làm bạn ta nhức đầu.
Bài toán tuổi thọ 263 năm chưa tìm ra lời giải

Trong nghành nghề dịch vụ toán học, bài tập về các số nguyên tố luôn luôn giữ mức độ nặng nề kỉ lục tuyệt nhất điển hình như bài toán về đưa thuyết ở trong phòng toán học tập Christian Goldbach đã trải qua trong cả 263 năm tuy thế vẫn chưa có một ai minh chứng thành công được vấn đề đó. Việc này cũng được liệt vào trong số những danh sách câu hỏi khó nhất cố giới.
Năm 1742, vào một bức thư gửi mang lại đồng nghiệp tại Thụy Sỹ, Goldbach đã đề cập đến những vấn đề tương quan đến thuyết số được phạt biểu: “Tất cả những số nguyên khi lớn hơn 2 mọi là tổng của 3 số nguyên tố”. Chẳng hạn: 35 = 19 + 13 + 3 xuất xắc 77 = 53 + 13 + 11.
Sau hơn 250 năm, mọi bạn đã thống nhất gọi nó là mang thuyết Goldbach tam nguyên và có nhiều nhà toán học xả thân nghiên cứu cố gắng nhưng cho đến lúc này thì vẫn chưa tồn tại một ai đưa ra được giải đáp của bài toán này.
Cho cho thời điểm bây chừ thì người được chỉ ra rằng tiếp cận sớm nhất với câu hỏi này là công ty toán học tập Terence Tao tới từ trường đại học California sống Los Angeles, Mỹ. Nhà toán học tập này đã chứng tỏ được mỗi số lẻ là tổng tối đa 5 số nhân tố và hi vọng là bạn dạng thân có thể giảm tự 5 xuống còn 3 để sở hữu được thành công tuyệt đối trước mang thuyết Goldbach sau này không xa.
Bài toán đơn giản “Ai giữ lại cá” nhưng mà khiến rất nhiều người bắt buộc chào thất bại trước Albert Einstein.

Vào cuối nuốm kỉ XIX, nhà bác bỏ học danh tiếng người Đức Albert Einstein đã giới thiệu một câu đố cùng ông quyết đoán chỉ gồm rất ít fan trên thế giới là có thể giải được bài toán này!
Đề bài toán:
Có 5 ngôi nhà, mỗi ngôi nhà được sơn bởi một màu khác nhau.
Chủ nhân của mỗi căn nhà này lại mang 1 quốc tịch khác nhau.
5 người sở hữu của ngôi nhà này thì mỗi người lại chỉ ham mê một các loại nước uống, hút một thương hiệu thuốc lá khác biệt và nuôi một con vật nuôi riêng.
Không gồm vị người chủ sở hữu nào lại ưa thích uống thuộc một một số loại nước uống, hút cùng một hãng dung dịch lá và gồm cùng một sinh vật nuôi.
Bài toán siêu hóc búa nhưng mà chỉ 0,001% bạn giải được
Bài toán vô cùng hóc búa này được xếp thứ hạng là trong những bài toán nặng nề nhất vậy giới. Trước tiên tiên, vấn đề này được gửi vào trong kỳ thi SAT năm 1982 với chỉ gồm 3 trong tổng cộng 300.000 sỹ tử tham gia chỉ dẫn câu trả lời chính xác.

Đề bài: Cho buôn bán kính hình tròn B cấp 3 lần chiều dài phân phối kính hình trụ A. Nếu hình trụ A lăn xung quanh hình tròn B thì nó phải thực hiện bao nhiêu vòng quay để có thể trở lại điểm xuất phát?
=> những phương án được đưa ra khiến cho thí sinh lựa chọn là 3/2, 3, 6, 9/2, 9 vòng.
Cả đa số thí sinh dự kỳ thi SAT năm kia và không ít người dân khi gọi đề thi này phần lớn chọn giải pháp số 3 là câu vấn đáp đúng.
Tuy nhiên, nếu lấy hệ quy chiếu là vòng tròn A thì nó chỉ tự quay quanh 3 vòng. Mặc dù thế nếu mang hệ quy chiếu ko nằm bên trên vòng A thì nó đã quay được 4 vòng, vòng sản phẩm công nghệ tư chính là do vòng tròn B khuyến mãi thêm.
Bài toán tra cứu sinh nhật của Cheryl tới từ Singapore

Đề bài:
Bernard và Albert vừa kết các bạn với Cheryl. Tìm ngày sinh nhật của Cheryl. Sau đó, Cheryl đã đưa ra 10 đáp án: Ngày 15/5, ngày 16/5, ngày 19/5, ngày 17/6, ngày 18/6, ngày 16/7, ngày 14/7, ngày 14/8, ngày 15/8 và ở đầu cuối là ngày 17/8. Sau đó, Cheryl đã bật mí riêng với Albert và Bernard về tháng với ngày sinh của phiên bản thân mình.
Albert: “Tớ đắn đo ngày sinh của Cheryl, tuy nhiên tớ biết chắn chắn Bernard cũng không biết”.
Bernard: “Trước tớ cũng không biết ngày sinh của doanh nghiệp ấy mà lại giờ tớ biết rồi”.
Albert: “Vậy tớ đang biết ngày sinh nhật thật sự của Cheryl”.
Vậy theo những bạn, Cheryl sinh ngày nào? Ngay sau thời điểm Alex Bellos đăng bài toán này lên The Guardian, hàng nghìn người đã bước đầu đi kiếm tìm kiếm đáp án. Bình luận được nhiều người để ý nhiều nhất đã thuộc về fan hâm mộ Colinus với thắc mắc thể hiện sự bất lực của anh ý trước việc đáng lẽ chỉ giành cho học sinh 14-15 tuổi: “Tại sao Cheryl ko nói thẳng ra luôn luôn sinh nhật của cô ấy ấy mang đến hai bạn?”.
Đây là một thắc mắc có vào đề thi của hội thi Olympic Toán học châu Á năm 2015, theo Mothership.sg. Thực ra, người ra đề chỉ mong kiểm tra kỹ năng suy luận của thí sinh tham gia chứ ko phải kĩ năng làm toán của họ.
Và đáp án đúng là sinh nhật của Cheryl là ngày 16/7 (July 16).
Bài toán tìm số áo của Mỹ năm 2014

Đây là bài toán được đưa ra trong hội thi Toán quốc gia mỹ năm 2014.
Đề bài:
Có ba thành viên trong nhóm bóng chày đàn bà trường trung học tập Euclid đang nói chuyện với nhau.
Xem thêm: Cách Dùng Vsco Trên Máy Tính Cực Nhanh, Cách Cài Đặt Vsco Trên Máy Tính
Ashley: Tớ vừa nhận biết số áo của 3 bọn mình phần đa là số nguyên tố có hai chữ số.
Bethany: Tổng hai số áo của chúng ta chính là ngày sinh của tớ vừa diễn ra trong tháng này.
Caitlin: Ừ, vui thật, thật trùng hợp khi tổng nhì số áo của các cậu lại là bao gồm ngày sinh của tôi vào cuối tháng này.
Ashley: với tổng số áo của tất cả hai cậu lại bằng đúng ngày hôm nay.
Vậy vào đội, Caitlin mặc áo số mấy?
(A) 13 (B) 11 (C) 17 (D) 19
Đây là 1 trong bài toán tương đối thú vị và cũng không thật khó để giải. Chính vì tất cả các ngày được nói đến trong mẩu truyện đều phía trong cùng một tháng, yêu cầu ngày sinh của Caitlin là bự nhất, có nghĩa là bằng 30, ngày lúc này là ngày 28 với ngày sinh của Bethany là 24. Từ đó thuận tiện tìm được số áo của Ashley đó là 13, của Bethany là 17 và còn Caitlin có áo số 11.
Bài toán về hiệp sĩ và kẻ dối trá của Liên Bang Nga
Những dạng việc về hiệp sĩ hết sức được yêu mến ở nước Nga. Trong một kỳ thi Olympic giành riêng cho những học sinh lớp 9, người ra đề đã giới thiệu một bài xích toán cực kỳ thú vị.
Cho 30 fan ngồi quanh 1 bàn tròn gồm 30 loại ghế được đánh số theo trang bị tự từ là 1 đến 10. Một số trong số chúng ta là hiệp sĩ, một vài lại là kẻ lừa dối. Hiệp sĩ luôn nói thật còn rất nhiều kẻ lừa dối thì luôn luôn nói dối. Mọi cá nhân chỉ tất cả đúng một bạn bạn trong các những người khác.
Hơn nữa, người chúng ta của hiệp sĩ lại là người lừa dối và bạn của kẻ lừa dối lại là hiệp sĩ. Mọi người sẽ rất nhiều được hỏi: “Có phải chúng ta của anh sẽ ngồi sát bên anh không?” 15 bạn khi ngồi ở phần lẻ trả lời: “Đúng”.
Tìm số người đang ngồi tại phần chẵn cũng giới thiệu câu trả lời: “Đúng”.
Tiến sĩ trằn Nam Dũng hiện đang là giảng viên Đại học kỹ thuật Tự nhiên, của Đại học nước nhà TP sài gòn đã gửi ra giải thuật đáp như sau: tự đề bài đã cho, ta có thể suy ra trong 30 người dân có đúng 15 cặp hiệp sĩ và kẻ lừa dối là bạn của nhau. Từ bỏ đó, ta hoàn toàn có thể dễ dàng tư duy được đáp số của câu hỏi này bằng phương pháp “giả định” cả 15 người tại đoạn lẻ đa số là hiệp sĩ. Lúc đó, dĩ nhiên bạn của những hiệp sĩ này đông đảo ngồi cạnh ở các vị trí chẵn với sẽ đều là người lừa dối, vị đó không người nào nói “Đúng”. Đáp số đúng là 0.

Tuy nhiên, đây chỉ là dự đoán đáp số của việc chứ chưa hẳn lời giải. Với phương pháp hỏi sinh hoạt đề bài, ta sẽ biết đáp số là 0. Dẫu vậy để xác minh được điều này, ta đề xuất phải chứng tỏ chứ phải không những là chỉ dẫn một ví dụ như vậy.
Nếu bọn họ quá sa đà vào việc xét địa điểm ngồi của tất cả 30 người (ai là hiệp sĩ cùng ai là người nói dối) thì sẽ rất rối bởi vì có rất nhiều trường hợp xảy ra. Tuyệt kỹ của giải mã ở đó là là ở thừa nhận xét đặc biệt quan trọng sau:
Trong 2 fan là các bạn của nhau thì chỉ có đúng 1 fan nói “Đúng” cho thắc mắc “Có phải bạn của anh vẫn ngồi ở bên cạnh anh không?”. Thật vậy, nếu có hai người, 1 hiệp sĩ và 1 kẻ lừa dối là các bạn của nhau. Xét 2 ngôi trường hợp:
Nếu họ ngồi cạnh nhau thì hiệp sĩ sẽ lên tiếng nói đúng, còn kẻ lừa dối sẽ nói “Không”.
Nếu họ không ngồi cạnh nhau thì hiệp sĩ đang nói “Không”, còn kẻ lừa dối đã nói “Đúng”.
Như vậy, chính vì ta gồm 15 cặp bạn bè nên ta sẽ có đúng 15 câu vấn đáp “Đúng”. Bởi vì cả 15 người tại đoạn lẻ phần nhiều đã nói “Đúng” nên toàn bộ những tín đồ ngồi ở vị trí chẵn số đông nói “Không”. Có nghĩa là đáp số của bài xích đưa ra bằng 0.
Vậy nên bài viết này shop chúng tôi đã cung cấp cho mình đọc rất nhiều bài toán nặng nề nhất vắt giới cũng như giới thiệu cho bạn sự thành lập của bắt đầu toán học.
Trả lời Hủy
Email của bạn sẽ không được hiển thị công khai. Những trường đề xuất được ghi lại *
Bình luận *
Tên *
Email *
Trang website
lưu lại tên của tôi, email, và website trong trình phê duyệt này đến lần phản hồi kế tiếp của tôi.
Toán học là môn học đòi hỏi tư duy logic. Mong mỏi học giỏi Toán cần học những kiến thức và kỹ năng nâng cao, làm cho những bài tập khó. Tuy nhiên, khi gặp mặt bài toán khó khăn nhiều học viên dễ chán nản chí, quăng quật qua. Nếu dễ dãi nản chí do vậy thì bạn sẽ không thể tiến bộ, không thể giỏi Toán.
Làm những việc khó là cách để học xuất sắc môn Toán
Luôn tìm kiếm tòi mở rộng kiến thức là trong những cách giúp bạn học giỏi môn Toán nhanh hơn. Lịch trình trong sách giáo khoa vốn là kiến thức chuẩn, căn bản. Muốn là một trong học sinh tốt Toán, ngoài việc làm rõ và cầm cố chắc kỹ năng và kiến thức trong sách giáo khoa, bạn cũng cần tìm tham khảo thêm sách tham khảo, sách nâng cao.
Đồng thời, yêu cầu làm bài xích tập thiệt nhiều, bước đầu từ phần nhiều bài đơn giản rồi đến những bài tập khó… việc làm bài xích tập nhiều sẽ giúp đỡ ta rèn luyện tứ duy nhanh, tích điểm thêm kiến thức bổ sung cập nhật cho lý thuyết. Đọc thêm các sách học viên mới cầm chắc với hiểu đúng, thâm thúy hơn những kiến thức trong sách giáo khoa.
Để rèn luyện biện pháp học xuất sắc môn Toán học sinh cần vắt vững các nguyên tắc: Trang bị kiến thức cơ phiên bản (nắm vững kiến thức và kỹ năng sách giáo khoa) -> Ôn luyện nhuần nhuyễn (sử dụng kiến thức và kỹ năng làm những bài tập cơ bản một bí quyết thuần thục) -> cải thiện (tìm tòi làm bài tập trong các sách nâng cao) -> năng lực tự tổng vừa lòng (tổng hợp kiến thức cho riêng mình) -> trở thành kiến thức sách vở và giấy tờ mình học thành nguồn của mình (bạn làm được điều này khi chúng ta cũng có thể giảng giải lại cho anh em một phương pháp lưu loát không phải dùng sách vở) -> bốn duy (khả năng làm những bài tập khó, không có dạng độc nhất định).
Tuy nhiên, tất cả những câu hỏi khó học viên mãi không kiếm ra cách giải, ko tránh khỏi bài toán nản chí, mong muốn từ bỏ. Nhiều học viên đăng trên các nhóm học tập nhằm được share kinh nghiệm khi đương đầu với một câu hỏi khó:
Cách giải pháp xử lý khi chạm chán bài toán khó
Có 2 trường hòa hợp xảy ra: gặp mặt bài toán khó khăn khi sẽ luyện tập, và chạm chán khi vẫn trong phòng thi.
Trường phù hợp 1: gặp mặt bài toán khó khăn khi sẽ luyện tậpMột ngày tất cả 24h, nếu dành thời gian suy xét quá những về một bài toán thì đang hại những lợi ít. Học tập sinh cần có sự phân chia thời gian đúng theo lý. đề nghị dành thời gian làm các bài tập dễ dàng hơn chứ tránh việc tốn không ít thời gian đến một việc khó mãi không kiếm ra lời giải. đa số khi bế tắc, chúng ta cần bài bác giải. Gồm nhiều cách để có bài bác giải như hỏi thầy cô, hỏi bạn bè, hoặc xem thêm bài giải trên trong sách, bên trên mạng. Xem xét không xào nấu y nguyên bài bác giải mà bắt buộc biến nó thành phương pháp giải của bản thân thì các bạn sẽ nhớ thọ hơn; không lạm dụng bài bác giải vày nếu cứ bài bác khó nhưng đi hỏi hay quan sát giải thì khối óc của chúng ta sẽ bị thui chột đi không nhiều nhiều.
Trường thích hợp 2: gặp mặt bài toán nặng nề khi đang trong chống thi.Trước hết, chúng ta nên yên tâm chứ tránh việc lo sợ, hoảng loạn. Trong chống thi, tuyệt đối không cần nghĩ đến công dụng kém như được điểm thấp, rớt kỳ thi do nó rất có thể làm chúng ta “quáng” hơn nữa. Tay nghề khi làm bài bác thi là phải làm trường đoản cú những bài bác dễ rồi mới đến các bài khó. Bởi thời gian trong chống thi là tất cả hạn, mỗi phút trôi qua đều rất quý giá cần phải tận dụng. Cùng với những việc khó, các bạn hãy bình tâm xem xét về phương pháp, kỹ thuật,… có thể áp dụng vào xem dòng nào phù hợp…

Để cách xử lý một việc khó, bạn cần phải có kiến thức căn nguyên trước. Bất kỳ vấn đề hay lĩnh vực nào, loài kiến thức căn nguyên không vững mà vội lăn tăn cách xử trí thì siêu dễ gặp khó khăn, từ kia bị xúc động, có cảm hứng như mình yếu thông minh, từ trách mình. Bởi vậy, trước tiên bạn hãy kiểm tra kiến thức nền tảng gốc rễ của bao gồm mình. Tiếp theo, khi sẽ có căn nguyên tốt, hãy liên tiếp va chạm… Khi gặp một vấn đề hay việc khó, bạn cũng có thể nghĩ cho hai câu hỏi sau để chế tạo ra động lực: vì sao người ta nghĩ được nhưng mà mình không cho là được? Đối với vấn đề khó như thế này, mình rút ra được mẫu gì?… các bạn phải luôn luôn giữ bình tĩnh, tỉnh táo bị cắn dở và quyết tâm. Giả dụ không, bạn sẽ không thể tiến bộ, ko thể giỏi Toán.
Bạn Đỗ Minh Khuê (Khánh Hòa) phân tách sẻ: “Mọi vấn đề đều phải sở hữu cách xử lý của riêng biệt nó nếu bạn chịu để ý đến và kiên nhẫn tìm ra nó”. Môn Toán đã hỗ trợ em thừa nhận ra điều ấy và giúp em suy xét sáng trong cả hơn. Mặc dù thuở đầu em thấy môn học này rất khó và dễ nản, nhưng sau khoản thời gian học trên chuyenly.edu.vn thì em thấy nó không khó như mình nghĩ, nhưng phải ghi nhận cách giải quyết bằng dòng đầu của mình”.
Để giúp câu hỏi học môn Toán của học viên đạt được tác dụng như hy vọng muốn, ráng chắc kỹ năng cơ bạn dạng và hoàn toàn có thể tự tin có tác dụng được những vấn đề khó, học viên và phụ huynh hoàn toàn có thể tham khảo chương trình Học giỏi 2020 – 2021 của chuyenly.edu.vn. Toàn bộ bài giảng trong chương trình đều có thiết kế theo chương trình sách giáo khoa hiện tại hành do cỗ GD&ĐT ban hành. Đội ngũ cô giáo tham gia đào tạo và huấn luyện đều có không ít năm kinh nghiệm và bao gồm những phương thức giảng dạy hiện đại, sáng tạo, kích thích tư duy của học sinh. Xung quanh ra, dịch vụ cung cấp Hỏi đáp 247 đang giải đáp, trao đổi vướng mắc của học viên trong mỗi bài giảng và cam kết hỗ trợ trong vòng 30 phút (kể tự khi phát sinh câu hỏi) trong các khung giờ cố định trong ngày. Nếu học viên đặt câu hỏi ngoài mốc giờ này, đang được cung cấp trả lời vào khung giờ gần tốt nhất kế tiếp.
Đăng ký chương trình Học xuất sắc 2020 – 2021Trang bị kiến thức trọn vẹn với khối hệ thống bài giảng bám đít SGK, thay thế sửa chữa việc học thêm.Hệ thống đề bình chọn và bài bác tập trường đoản cú luyện bao gồm ĐÁP ÁN với HƯỚNG DẪN GIẢI.Đội ngũ giáo viên xuất sắc chuyên môn và giàu kinh nghiệm giảng dạy.Giúp học viên tăng cơ hội giành điểm 9 – 10 trong những bài thi, bài kiểm tra. |














